本文转载自微信公众号“人机与认知实验室”(ID: 9h_9c3c1f805cb8),作者 Kurt Ammon
1 介绍
Turing[8]引入了计算机(computing machine)的概念,后来被称为TuringMachine(图灵机)。他证明了Hilbert(希尔伯特)的可判定问题(Entscheidungsproblem)是无法解决的,也就是说,任何图灵机都不能决定:一个给定的符合一阶逻辑演算形式(数论中的数学问题)的陈述是否能被证明。Wegner写到,图灵对于可计算内容的精确描述确定并稳固了计算机科学作为一个学科的地位。他(Wegner)提出交互机(Interaction Machines)的概念并且表明,当计算延伸到交互作用领域时,图灵机不能获取关于“计算机所计算对象”的直观概念。他的交互机曾被评价是一个不必要的库恩范式转移[12]。Prasse和Rittgen[7]引用了Wegner的“交互机不能计算非递归的函数,所以Church的命题仍然成立。”这意味着交互机不能“计算”无法被图灵机计算的函数。
本文证明了不存在图灵机能在自然数集合上产生所有可计算函数的序列。证据表明了某种如果不与其环境分离开就不能被建模为预先定义的图灵机的 “可计算”系统的存在。大概来说,这些系统与环境进行交互来改变它们有限的描述,其中环境的发展由于实践或理论的原因而是不可完全预测的。我在论证,这个证明甚至可以应用到已经存在的系统,比如因特网。最终,我通过要求一类系统有能力去“计算”图灵机无法计算的函数,以此引入了这种新类型的系统。
一个可计算函数是指可以被图灵机计算的函数,也即,可以被一般的计算机程序描述。因此,一个可由自然数集合计算到自然数集合的程序可以被认为是一个能由输入区的任何自然数产生一个自然数来输出的计算机程序。一个这样的函数的例子是f(n)=n+1,它可以产生紧随任何自然数n的自然数n+1。
可以在自然数集合内计算的函数被认为是计算机程序和系统的模型。将可计算函数限制在自然数集合范围内是无关紧要的,因为计算机程序和系统的输入和输出都被表示为二进制数。有用的程序和系统应该工作于已定义的输入集,这些已定义的输入集对应于自然数集合的子集。通过对没有被程序和系统定义的输入来假设一个默认的输出,所定义这个输入集可以被延伸到所有的自然数,而不仅仅是子集。一般来说,一个程序或者系统是在一系列可判定的输入集合上得以界定的,也就是说,有一个程序用来判断一个输入是否可被程序接受来进行计算。因此,自然数集上的可计算函数是一类重要的计算机程序和系统模型。
不完全定理:没有图灵机可以产生从自然数集合N到自然数集合N的所有可计算函数f1,f2……
证明:我们假设有这样一个图灵机。我们定义一个新的在自然数集合范围内可计算的函数g,其中对于所有的自然数n都有g(n)=fn(n)+1。因为根据我们最开始的假设,函数集f1,f2……包括所有的可计算函数,所以存在一个自然数n使得g(x)=fn(x)对于所有自然数x皆成立。这立即产生了因为函数g的定义而导致的g(n)=fn(n)和g(n)=fn(n)+1的矛盾。这意味着我们最开始的假设是错误的,也就是说,没有图灵机可以产生自然数集合范围内的所有可计算函数集f1,f2……
在证明中的可计算函数g的构造可以被图灵机T代表。当然,T可以被纳入任何图灵机。证明表明,无论T被怎样纳入图灵机,没有图灵机可以产生所有可在自然数集合范围内计算的函数集f1,f2……特别是,T可以被纳入在证明中被假设存在的图灵机,这种情况下延伸的图灵机可以产生函数集f1,f2,……和g。但是延伸的机器与原始的机器不同,因此它的应用会与我们的假设,即一个图灵机可以产生所有可在自然数集合范围内计算的函数,相矛盾。
因为任何形式系统都可以简单地被定义为一个定理证明图灵机(例子见 [4, p. 72]),这也表明任何的形式理论在它不能“捕获”所有自然数集合范围内可计算函数的这个意义上说是不完全的。
让C成为一个有能力执行推理过程的系统,这种能力被需要用来证明我的简单的不完全性定理。因此,C有能力构造一个可在自然数范围内计算的函数g,且这个函数不是被任何给定的图灵机M所产生的。图1在C能够制造出来的自然数集合上说明了相符的证明——没有被预先定义的图灵机M可以产生所有的在自然数范畴内可计算的函数f1,f2……
一个在C和图灵机之间的区别是C不能被认为成是静态的、被提前定义的、与它所在环境隔离开来的东西。相反,在证明中的C和图灵机M,在“C假定一个可产生所有自然数范围内可计算函数集f1,f2……的图灵机M存在,目的是为了构造一个可计算的不被M产生的函数g”的意义上,被认为成是分离的实体。粗略地说,C可以通过与它的环境交互改变它自己(也就是图灵机M)。
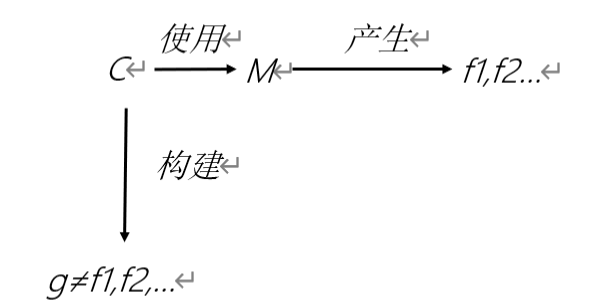
图1: 证明
因为C的构建可计算函数的能力不能被任何提前定义的图灵机模拟,似乎就需要有另一个关于此种系统的模型。
可计算函数可以被图灵机或者计算机程序表示,也就是,它们有有限的描述。这样的描述的集合可以被有效地列举。这意味着有一个图灵机可以产生一个包含所有有限描述的序列,比如升序排列。因为这些原因,我的简单的不完全性定理表明:“判定一个被给出的描述能否代表一个在自然数范围内的可计算函数”是不可计算的。如果这种功能可以被计算,那它对于一个有效枚举或有效描述的应用将会产生一个对于自然数范围内所有可计算函数的有效枚举。这与我的定理相矛盾。因此,没有图灵机可以决定一个被给出的描述是否是一个可计算的函数,也就是说这个可判定问题(Entscheidungsproblem)是不可解决的。
而且,我的简单不完全性定理表明,那些有能力证明这个定理的系统,在它们可以超越任何被提前定义的图灵机的限制,来构造更多强有力的、可在自然数范围内计算的函数的意义上,似乎有能力解决上述的可判定性问题。这意味着以下对于新类型系统的定义:
定义:一个系统如果有“计算”不可计算函数的能力,也就是说它可以对给定参数下的不可计算函数以决定值,那么它是有创造力的。
关于这个定义,创造性系统可以包含任何可计算函数。因此,从能“计算”可计算函数和不可计算函数的意义上讲,它们可以被认为成是图灵机概念上的延伸。
一个创造性系统的结构是在与SHUNYATA (空性)程序[1,2]的实验上的基础上被发展起来的。它是通往一个创造性系统实施的第一步。粗略地说,一个创造性系统包括一个映射基础和不同数量的不断演化的分析空间。
定义:映射基础包括一个通用的程序性语言,初级的特定领域的概念,以及关于这个语言和这些概念的知识。
因为所有的可计算函数可以被一个通用的程序性语言表示,我的简单不完全性定理表明映射基础不能被完全形式化。
定义:分析空间包括部分知识,这些知识的应用领域被限制但是通常在分析空间的发展中是扩张的。
粗略地说,在创造性系统中新的知识的发展可以被总结成如下几个原则:
发展原则:
1.分析空间中的知识产生于映射基础和先前的知识。
2.知识的发展包括新的分析空间的发展和已经存在的空间的合一。
3.新知识的合算变化倾向于被保护,而不合算的倾向于被摧毁。
比如,映射基础可能包括常量的基础知识和一个编程语言的功能。
一个非常简单的程序任务是一个产生任何一个输入的自然数n的下一个数n+1的构造。这个程序可以在初级知识“1是一个自然数”以及“当x和y是任意的自然数时,x+y是一个自然数”的基础上被构造出来。
另一个简单的例子是一个快速排序的程序sort (L),该程序可以对于一个列表L里的元素,在任何元素x和元素y之间,根据一个给定的顺序关系“x小于y”进行排序。这样的一个程序的核心可以被程序性伪码表示:
append(
sort(x∈ L : x <first(L)),//对L中比L首个元素小的所有元素排序
first(L),//L的首个元素
sort(x ∈ L : first(L) < x))//对L中比L首个元素大的所有元素排序),--------(1)
译者注:快速排序的思路在于通过不断比较进行范围划分和不同层次范围内的调整,即同一简单方法在不同层次的“分而治之”。
这个append函数追加了列表,而first(L)是列表L的第一个元素。为了给列表L排序,程序给比它第一个元素小且属于L的元素和比它的第一个元素大且属于L的元素进行分类。对于这个“分类和占据”的方法的递归应用,产生了越来越小的部分列表或者不需要被排序的空列表。最终,通过连续添加所有以前排好序的部分的列表,产生一个包括L中所有元素的排好序的列表。
快速排序的程序也可以在关于它包含的函数的初级知识的基础上被构造。粗略地来说,这个知识仅仅需要给出函数的领域和范围,也就是函数的定义域和呈现的值域。比如,(1)中的命题x小于first(L)可以在“first(L)是一个L的元素”以及“x小于y是一个对于任何属于L中的x和y成立的命题”这两个知识的基础上被建立。快速排序程序(1)中函数的有效选择似乎是可行的,因为它们非常基本,如append函数,甚至编程任务中显式包含的函数,如顺序关系“<”。
例如,SHUNYATA(空性)程序通过在关于组成程序函数的基本知识[1]的基础上分析简单定理的证明,产生了定理证明程序。这些程序的发展,说明了以上被给出的这些准则的非常简单的方面,比如分析空间的统一以及合算变化的产生。由SHUNYATA发展的定理证明程序带来了其他理论的证明,特别是,一个关于SAM’s Lemma的证明,它的证明比其他任何以前知道的证明更简单。SAM’s Lemma的复杂性或多或少代表了自动化理论证明艺术的状况[1,p. 561]。
哥德尔(Go¨del)的不完全性定理说道,所有的形式数字理论包括一个不能解决的命题,也就是说,命题和它的否定都在其理论中不可被证明。关于哥德尔理论的证明中,主要的问题就像是这样的命题的构建。类似于快速排序程序(1)的构造,一个不能被决定的命题可以在公式信息的基本规则的基础上被构造,也即,在命题所包含符号的基本知识的基础上。Ammon[2]描述了哥德尔(Go¨del)定理的证明,并引用了SHUNYATA程序的进一步实验。
4 讨论
因特网是一种有着变化数目的计算机程序和系统的网络。我的简单不完全性定理表明:没有预先定义的形式系统能够完整地建模如此的网络,因为程序(可计算函数)不能被这个形式系统所“捕获”而加入到网络中。我的理论证明表示这种构建程序的过程可以被自动完成。
有能力比存在的系统更自然地与人类相互交流、交互的系统应该有能力重新构建在人类交流形式中潜在使用的可计算函数。我的理论表明:不存在可以被预先定义的图灵机或者形式系统能模拟这种交流。
计算机程序必须在他们可以被用在实际中前被测试和调试。我的理论表明没有普遍的被预先定义的用来证实程序的算法,因为一个不被算法捕获的程序可以从算法本身构造。然而,程序的证实要在经验的基础上达成。
在我的不完全定理中的证明中产生一系列可计算的函数f1,f2……的图灵机可以被认为成一个分析空间。另一个产生f1,f2……的图灵机的构造和一个可计算的不被原始机器产生的函数g可以被认为成新的分析空间的构造。因此,我的简单理论表明所有的分析空间不能被统一成一个单独的分析空间。粗略地说,在分析空间的新知识的发展不能被认为成完全可描述的“密闭箱“。相反,它是一个开放的、可以超越任何被事先指定好的构架的过程。
我的研究也可以被认为成是一个关于在计算机的帮助下来进行的关于为什么“因为创造性的系统可以超越任何被预先定义的算法,来决定一个以一阶逻辑演算形式的陈述句是否可以被证明,所以希尔伯特的决定问题是不可解决的。”的调查,
Church的理论声称任何可有效计算的函数是普遍递归的[5,pp. 317-323]。与Church的理论相当的图灵理论,声称任何可以被顺理成章地认为成可计算的函数,在他的定义下都是可计算的,也就是通过图灵机[5,pp. 376-381]。我的研究不应该被认为是对于Church或者图灵的理论的驳斥。相反,它让这些理论和Hilbert的决定问题被人们所知道。特别是,它证明了,如果在“计算”意味着决定被给出论题的函数值的情况下,可以“计算”不可计算函数的系统的的存在性。但是这些系统没有可以预先给出的完整有限描述。相反,它们可以超越任何被预先定义的形式化描述。
图灵[9,10]讨论到是否“有可能让机器展现智能行为”。参考哥德尔(Go¨del)和其他的在相似方面的理论,由Church,Kleene, Rosser ,和他自己得出结果,图灵[9,p.445]写到:“任何专用机器的能力都存在限制”。
图灵[10,p.4]声称:
来自哥德尔(Go¨del)和其他种种理论的辩论本质上可以以“机器不能犯错”为条件而停下。但是这并不是智能的要求。
他声称“一个被提供纸、笔、橡皮擦和严格规则的人”可以“产生一个计算机器的效果”,但是“规则本身对于产生智能当然是不够的” [10, p. 9 和 p. 21].。我的简单不完全定理确认了任何特殊的图灵机的能力是受限制的。定理表明有能力证明定理并能与环境交互的系统是不能被任何提前定义好的图灵机模拟的。因此,具有一定证明定理和与环境交互能力的“一般计算机系统”原则上可以在能力上超越任何被事先设定好的机器。我的定理表明像这样的系统必然以经验为依据,并且是不可靠的。这种不可靠是在以下感知下成立的:关于价值判断,形成对其完全预先定义的形式化(例如,一个被给定的计算机程序是否代表一个自然数范围的可计算函数?)是不可能的。
我的关于创造性系统的定理和原则和Post的观点[6, p. 417]是相一致的:
…逻辑一定…在它的运作中变得非形式化。更好的是,我们写到:
逻辑的过程必须是有创造性的
Wegner[11]认为“交互比算法更加强有力。”我的简单不完全定理可以被认作是一种对他的理论的数学上的证明。更重要的是,这个定理和它的证明表明可“计算”不可计算函数的系统的存在性,也就是决定对于被给出的论题的不可计算的函数的值。在这种意义上,它们确认了Wegner和Goldin[12]的观点——“逻辑和算法都不能完全复制计算机和人类的想法。”
Wegner[11]写到交互机(interactionmachines)的不完全性遵循“动态产生的输入流在数学上被以有限字母表为基础的无限序列模拟,这是无法列举的。”这一事实。这里的“不完全性”根据定义并非创造力系统的不确定。这更多的是来源于这样的事实:没有形式化的理论可以“捕获”所有自然数集合下的可计算函数。
我的不完全性定理表明没有普遍的算法或者形式系统用来核定程序。这个结果是与Wegner的“证明正确性不仅仅是困难的,更是不可能的”的观点相符的,因为“开放的、以经验为依据的、可证伪的或者交互的系统一定是不完整的”[11,p. 10]。它也和哥德尔(Go¨del)的陈述[3, p. 84]"人们只能根据给定的语言来定义它们[可论证性和可定义性]",也就是说,没有关于形式证明的普遍定义,但这样的定义可以只在特殊的形式系统中被给出。
[1] Ammon, K. The automaticacquisition of proof methods. Proceedings of theSeventh National Conference on Artificial Intelligence, St. Paul, U.S.A, August 1988.Morgan Kaufmann, San Mateo, Calif., USA.
[2] Ammon, K. An automatic proof of Go¨del’sincompleteness theorem. Artificial Intelligence 61, 1993, pp. 291–306. ElsevierScience Publishers (North-Holland), Amsterdam.
[3] Go¨del, K. Remarks Before the PrincetonBicentennial Conference on Problems in Mathematics. In M. Davis (Ed.), TheUndecidable, Raven Press, New York, 1965.
[4] Go¨del, K., On undecidable propositions of formalmathematical systems- POSTSCRIPTUM. In M. Davis, The Undecidable, Raven, Press,New York, 1965.
[5] Kleene, S. C. Introduction to Metamathematics.Wolters-Noordhoff, Groningen, and North-Holland, Amsterdam, 1952.
[6] Post, E. Absolutely Unsolvable Problems and Relatively UndecidablePropositions - Account of an Anticipation. In: M. Davis (Ed.),The Undecidable, Raven Press, New York, 1965, pp. 338–433
[7] Prasse, M., and Rittgen, P. Why Church’s Thesis Still Holds. Some Notes onPeter Wegner’s Tracts on Interaction and Computability.The Computer Journal, Vol 41, No. 6, 1998.
[8] Turing, A. M. On computable numbers, with anapplication to the Entscheidungsproblem. Proceedings of the London MathematicalSoci-ety, Ser. 2, Vol. 42, 1936-37, pp. 230–265. Correction, ibid., Vol. 43,1937, pp. 544–546.
[9] Turing, A. M. Computing Machinery and Intelligence. Mind 59, No. 236, 1950, pp. 433–460.
[10] Turing, A. M. Intelligent Machinery. In: B.Meltzer and D. Michie (Eds.), Machine Intelligence 5, Edinburgh UniversityPress, Edinburgh, 1969, pp. 3–23.
[11] Wegner, P. Why Interaction is More Powerful thanAlgorithms, Com-munications of the ACM 40 (5), 1997.
[12] Wegner, P., and Goldin, D. Computation BeyondTuring Machines, Communications of the ACM 46 (4), 2003.
